Haskell Hero

Haskell Hero es un manual interactivo del lenguaje Haskell para principiantes.

Funciones

<= Evaluación lección anterior lección siguiente Trabajamos con un script =>

La función como una caja

En el modelo de cajas representamos funciones con cajas. Más exactamente con una caja en la que introducimos algo, la agitamos y después cae el contenido de la caja.

Por ejemplo podemos tener una función 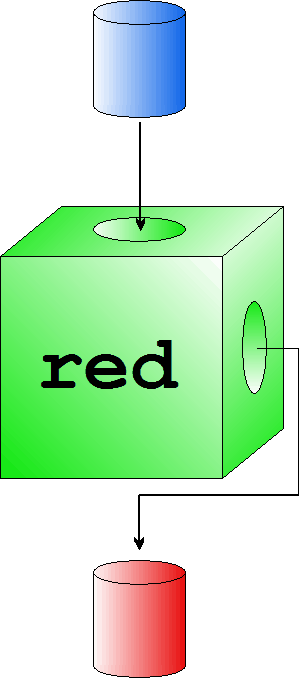red, en que ponemos un cilindro, la función le pone un color rojo y nos da el cilindro rojo como el resultado.

La representación de la función red

La mayoría de las funciones que vamos a usar trabaja con números o listas. Por ejemplo la función (+) toma dos números y nos da su suma.

La representación de la función (+)

La definición de funciones propias

La base de la programación funcional es la definición de funciones propias.

La definición de función tiene dos partes, la derecha y la izquierda, separadas con el signo igual.

La parte izquierda consta de un nombre de función y de sus parámetros. Los parámetros se escriben como cadenas de caracteres empezando con letra minúscula, generalmente solo en minúsculas.
En la parte derecha está el resultado de la evaluación de la función después de un paso.

Ejemplo:

Definimos una función plus3 que toma tres números y nos devuelve su suma. Queremos que por ejemplo su aplicación a números 5, 1 y 2 evalue a:

plus3 5 1 2  ~>  5 + 1 + 2  ~>*  8

Su definición podría ser esta:

plus3 x y z  =  x + y + z

Ejemplo:

Definid una función perimetroRectangulo que toma las longitudes de los lados de un rectángulo y devuelve el perímetro del rectángulo. La aplicación de la función por ejemplo a las longitudes 5 y 3 debería ser de esta manera:

perimetroRectangulo 5 3  ~>  2 * (5 + 3)  ~>*  16

Si sustituimos los parámetros reales 5 y 3 por parámetros formales a y b, llegamos a una definición general:

perimetroRectangulo a b  =  2 * (a + b)

Definición con patrones

Ejemplo:

Definamos una función numeroPalabra que toma un parámetro - un número entero.

Si toma un número 1, devuelve la cadena "Uno".
Si toma un número 2, devuelve la cadena "Dos".
Si toma un otro número, devuelve la cadena "Desconocido".

Una opción como definir la función es esta:

numeroPalabra x = if x == 1 then "Uno"
                            else if x == 2 then "Dos"
                                           else "Desconocido"

Es evidente como Hugs va a evaluar la expresión numeroPalabra 2. Sustituye x por 2 y la expresión numeroPalabra 2 reemplaza por la parte derecha de la definición, es decir con esta expresión:

if 2 == 1 then "Uno"
          else if 2 == 2 then "Dos"
                         else "Desconocido"

Después evalúa la condición 2 == 1 a False y toda la expresión la evalúa a la expresión en la parte else.

if 2 == 2 then "Dos"
          else "Desconocido"

La expresión 2 == 2 se evalúa a True, entonces toda la expresión se evalúa a la cadena "Dos".

La segunda opción es definir funciones con patrones. La misma función se define con patrones de la manera siguiente.

numeroPalabra 1 = "Uno"
numeroPalabra 2 = "Dos"
numeroPalabra x = "Desconocido"

Hugs va a evaluar numeroPalabra 2 de manera siguiente:

Prueba si se puede sustituir la parte izquierda de la primera ecuación numeroPalabra 1 por numeroPalabra 2. No se puede, entonces sigue con la segunda ecuación.
Prueba si se puede sustituir la parte izquierda de la segunda ecuación numeroPalabra 2 por numeroPalabra 2. Sí, se puede.
La expresión numeroPalabra 2 se sustituye por la parte derecha de la segunda ecuación, es decir, por la expresión "Dos".

¿Cómo se evaluaría la expresión numeroPalabra 5?

¿Se puede sustituir numeroPalabra 1 por numeroPalabra 5? No, vamos a probar la segunda ecuación.
¿Se puede sustituir numeroPalabra 2 por numeroPalabra 5? No, vamos a probar la tercera ecuación.
¿Se puede sustituir numeroPalabra x por numeroPalabra 5? Sí, se puede.
Sustituimos x por 5 y la expresión numeroPalabra 5 se sustituye por la parte derecha de la ecuación, es decir, "Desconocido".

Ya que el parámetro x no se usa en la parte derecha, en vez de x podemos escribir _ (n guión bajo), lo que significa "se puede sustituir por cualquier cosa que se después olvidará". Nuestra función entonces sería esta:

numeroPalabra 1 = "Uno"
numeroPalabra 2 = "Dos"
numeroPalabra _ = "Desconocido"

En Hugs el orden de definiciones de funciones no importa. Esto significa que si escribimos en el script

multiplicado 0 _ = 0
multiplicado x y = mas y (multiplicado (x - 1) y)


mas x y = x + y

la aplicación de multiplicado 3 2 nos devuelve el producto bien calculado de 3 y 2, lo que es 6. Sin embargo, ¡tened cuidado con el orden de ecuaciones! Como ya hemos mencionado arriba, cuando Hugs evalúa una función, prueba las ecuaciones sucesivamente. Si cambiásemos el orden de las ecuaciones de la función multiplicado así:

multiplicado x y = mas y (multiplicado (x - 1) y)
multiplicado 0 _ = 0

el cálculo no terminaría nunca, ya que Hugs siempre usaría la primera ecuación para la evaluación y la recurrencia sería infinita.

La definición recursiva

Ejemplo:

Definamos la función suma que toma un número natural y devuelve la suma de todos números naturales que son inferiores o equivalentes al número indicado. Un ejemplo de la evaluación:

suma 3  ~>*  3 + 2 + 1  ~>*  6

Ya que sabemos como escribir definiciones con patrones, podemos definir la función suma para números de 1 a 5 de manera siguiente:

suma 1  =                  1
suma 2  =              2 + 1
suma 3  =          3 + 2 + 1
suma 4  =      4 + 3 + 2 + 1
suma 5  =  5 + 4 + 3 + 2 + 1

Sin embargo, nosotros necesitamos una definición general que nos permitiría evaluar la función suma con todos números naturales. En este momento nos viene bien la recursión.

En una palabra, la función recursiva es una función que evalúa a una expresión que la contiene sí misma.

Si miramos la definición de suma 4, podemos ver que consta de la función (+), el parámetro 4 y la expresión 3 + 2 + 1 que se puede escribir como suma 3. De esta manera podemos escribir las cinco ecuaciones:

suma 1  =  1
suma 2  =  2 + suma 1
suma 3  =  3 + suma 2
suma 4  =  4 + suma 3
suma 5  =  5 + suma 4

De esta notación ya podemos deducir la definición general de la función suma:

suma x = x + suma (x - 1)

Sin embargo, si dejamos Hugs evaluar la expresión suma 3, Hugs va a calcularlo y después nos va a decir que la pila está llena. ¿Por qué ocurrió esto? Escribamos la evaluación de la expresión suma 3:

suma 3

~>  3 + suma 2
~>  3 + 2 + suma 1

Queremos que el cálculo se termine en ese momento. Pero según la definición, el cálculo va a seguir:

~>  3 + 2 + 1 + suma 0
~>  3 + 2 + 1 + 0 + suma (-1)
~>  3 + 2 + 1 + 0 + (-1) + suma (-2)
~>  ...

Por eso tenemos que añadir a la definición un caso base que sustituye suma 1 por 1 y así finaliza la llamada recursiva. La definición correcta de la función suma sería entonces la siguiente:

suma 1 = 1
suma x = x + suma (x - 1)

Nota

Ya que la recursividad se usa con frecuencia en la programación funcional, hay muchas librerías con funciones que hacen la recursividad en vez de nosotros. A partir de estas funciones sencillas después podemos componer funciones más complejas.

Definición local

Ya sabemos como definir nuestra propia función. ¿Pero cómo pasamos la definición a Hugs? Tenemos dos opciones. Podemos definirla localmente o globalmente. En este párrafo vamos a ver la definición local.

Definiciones locales se escriben en esta forma:

let definición in expresión

En lugar de definición se escribe la definición de una función o una constante y en vez de expresión se escribe la expresión que se después evalúa usando la definición en la parte definición. La definición se llama local porque es válida solo en la parte expresión de la let-expresión correspondiente.

Ejemplos:

let cinco  =  5 in 5 + cinco  ~>  5 + 5  ~>  10
let mas3 x y z  =  x + y + z  in  mas3 1 3 5
    ~>  1 + 3 + 5  ~>*  9

Si necesitamos definir más de una función o una constante en una let-expresión, las pondremos entre llaves y las separaremos con punto y coma.

let {dos = 2; tres = 3; cinco = 5; mas3 x y z = x + y + z}
    in mas3 tres cinco dos
~> 3 + 5 + 2 ~>* 10

La otra notación posible sería la con la palabra where. Se usa de manera siguiente:

expresión where definición

y funciona de misma manera como la let-expresión.

Ejemplo:

mas3 1 3 5 where mas3 x y z = x y z

<= Evaluación lección anterior lección siguiente Trabajamos con un script =>