 Haskell Hero
Haskell Hero
Haskell Hero es un manual interactivo del lenguaje Haskell para principiantes.
|
|
Funciones útiles IidLa función unaria que devuelve el parámetro sin cambios. Definición
id :: a -> a id x = x Ejemplo de uso
id 5 ~> 5 id "hola" ~> "hola" (id even) 3 ~> even 3 ~> False Un ejemplo más complejo
comp :: Int -> (a -> a) -> a -> a comp 0 _ = id comp n f = f . comp (n-1) fLa expresión comp n f x se evalúa de esta manera: Al elemento x se aplica n-veces la función f. La función id funciona aquí como un caso base cuando el valor del primer parámetro llega a ser cero.
comp 5 (+2) 10 ~>* ( (+2) . (+2) . (+2) . (+2) . (+2) . id ) 10El operador (.) se describe en el último párrafo.
constLa función binaria que devuelve su primer parámetro sin cambios. Definición
const :: a -> b -> a const x y = x Ejemplos de uso
const 5 'q' ~> 5 const True (+8) ~> True (const div "ffuu") 10 3 ~> div 10 3 ~> 3 Más informaciónLa expresión (const div "ffuu") 10 3 se evalúa de manera siguiente:
flipLa función ternaria que toma como parámetros:
La función flip cambia el orden del segundo y del tercer parámetro y estos parámetros pasan para la evaluación a la función Definición
flip :: (a -> b -> c) -> b -> a -> c flip f x y = f y x Ejemplo de uso
flip (-) 3 5 ~> 5 - 3 ~> 2 flip const True "sí" ~> const "sí" True ~> "sí" Operadores para la construcción de tuplas
Ejemplo de uso
(,) 5 True ~> (5, True)
(,,) "aAa" 5.0 False ~> ("aAa", 5.0, False)
fstLa función que devuelve el primer elemento de una dupla. Definición
fst :: (a,b) -> a fst (x,_) = x Ejemplo de uso
fst ("#&!",10.5) ~> "#&!"
sndLa función que devuelve el segundo elemento de una dupla. Definición
snd :: (a,b) -> b snd (_,y) = y Ejemplo de uso
snd ("#&!",10.5) ~> 10.5
Composición de funciones Composición de funciones en el modelo de cajas
Para la composición de funciones usamos el operador ternario
Los parámetros del operador
El resultado del cálculo es el parámetro tras las aplicaciones de funciones Definición
(.) :: (b -> c) -> (a -> b) -> a -> c (f . g) x = f (g x) Ejemplo
Definid la función binaria
sndOdd ("hola",5) ~>* True
sndOdd (True,8) ~>* False
La función toma una dupla de cualquier cosa y un número entero y devuelve sndOdd :: (a,Integer) -> BoolUna de las opciones es usar la definición con patrones: sndOdd (_,y) = odd yNosotros vamos a ver cómo podemos definir esta función con la composición de funciones. Queremos crear una función representada por la caja azul de la imagen arriba. Ponemos una dupla en la caja y Bool se cae de la caja.
Primero extraemos el segundo elemento de la dupla con la función snd (x,y)Después aplicamos la función odd al resultado:
odd (snd (x,y))Este podemos escribir con el operador (.) como una función compuesta. La definición final será la siguiente:
sndOdd (x,y) = (odd.snd) (x,y)Si podemos poner el parámetro de la función completamente a la derecha, podremos omitirlo en la definición. Esta notación la llamaremos pointfree (libre de puntos). La conversión de la función al estilo pointfree la vamos a describir más tarde. Ahora es suficiente saber que la notación siguiente es sustituible por la anterior. sndOdd = odd.snd 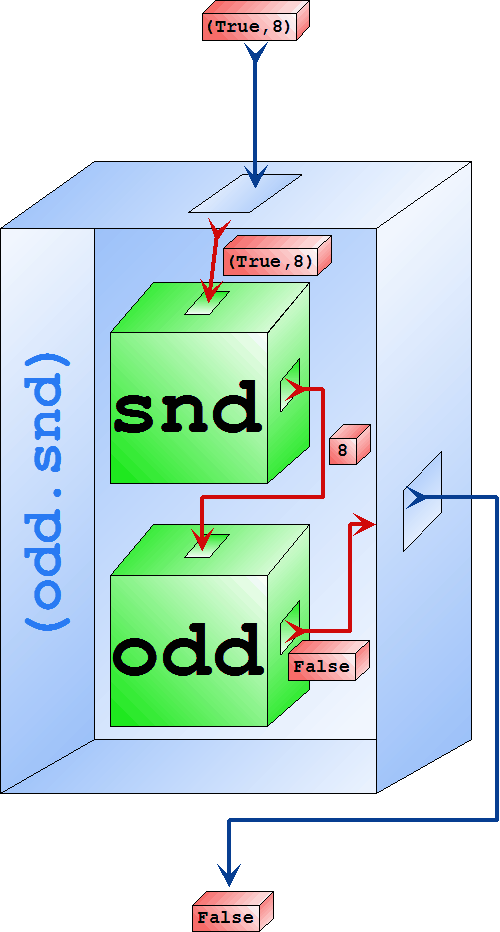 La evaluación de la expresión (odd.snd) (True,8) |