Haskell Hero

map es una función binaria que toma como parámetros:

• una función f que toma a y devuelve b
• una lista s de tipo [a] con elementos a los que se puede aplicar la función f

La expresión map f s se evalúa a la lista s con sus elementos, a los que fueron aplicados la función f, de tipo [b].

Definición

map         ::  (a -> b) -> [a] -> [b]
map _ []     =  []
map f (x:s)  =  f x : map f s

Ejemplos

map (+1) [1,2,3]  ~>* [2,3,4]
map even [1,2,3]  ~>* [False, True, False]
map (*8) []       ~>* []

Ejemplo de evaluación

Ahora llegamos al momento cuando vamos a usar la comparación de la lista con el tren. Si imaginamos la lista como un tren, la función map es un túnel.

El modelo de tren	Haskell
Tengamos una función carga que si toma un coche vacío, lo carga de carbón y si toma un coche lleno, lo deja lleno.	Tengamos una función carga que está definida de manera siguiente: carga :: Bool -> Bool carga False = True carga True = True
El túnel funciona de manera siguiente: Si hay un coche en él, lo carga de carbón y mueve el tren. Si hay una locomotora en él, la deja pasar y termina su actividad.	La función map funciona de manera siguiente: Si toma una función f y una lista no vacía x:s, aplica la función f al primer elemento de la lista, es decir, a x, el resultado lo pone al principio de la lista final y sigue con la aplicación de la función map al resto de la lista s. Si toma una cualquier función y una lista vacía, se evalúa a una lista vacía.
Pongamos entonces al túnel un tren que tiene tres coches vacíos.	Apliquemos entonces la función map a la función carga y a la lista [False,False,False].
En el túnel hay un coche vacío, así que se carga de carbón y el tren se mueve.	Ya que el segundo parámetro es una lista no vacía, evaluamos según la segunda ecuación de la función map. Aplicamos la función carga al primer elemento de la lista, lo que es False. Este se convierte en True, lo enganchamos al principio y seguimos con la evaluación de map carga [False,False].
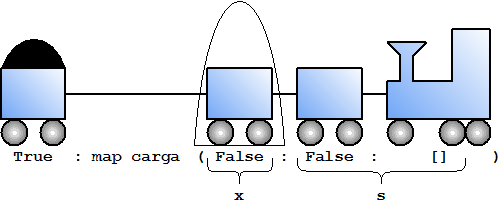
En el túnel hay un coche vacío, así que se carga de carbón y el tren se mueve.	Seguimos evaluando según la segunda ecuación. La variable x se sustituye por False, s se sustituye por [False]. Al principio se engancha carga False, lo que se evalúa a True, y se sigue con la evaluación de map carga [False].
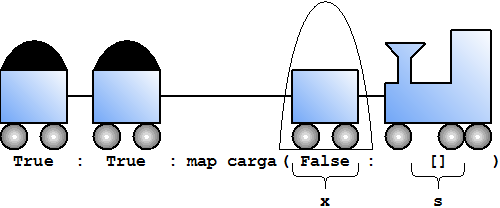
La misma situación, el coche vacío se carga de carbón y el tren se mueve.	Otra vez evaluamos según la segunda ecuación. x se sustituye por False, s se sustituye por [], así que la evaluación es la siguiente: map carga (False : []) ~> (carga False) : map carga []
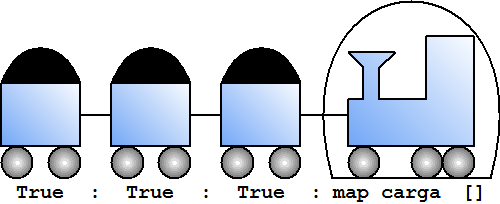
En el túnel está ahora la locomotora que sólo pasa y ya está.	La expresión map carga [] se evalúa a una lista vacía según la primera ecuación.
El resultado es un tren con tres coches cargados.	El resultado es la lista de tres elementos [True,True,True].

filter es una función binaria. Toma como parámetros:

• Una condición p, es una función que toma cualquier unidad y devuelve un valor booleano, entonces es de tipo a -> Bool
• Una lista s de elementos que puede tomar la función p, de tipo [a]

La expresión filter p s se evalúa a una lista de los elementos de la lista s que cumplen la condición p.

Definición

filter         ::  (a -> Bool) -> [a] -> [a]
filter _ []     =  []
filter p (x:s)  =  if p x then x : filter p s
                          else     filter p s

Ejemplos

filter (>5) [1,6,2,8,5,7]       ~>*  [6,8,7]
filter even [1,6,2,8,5,7]       ~>*  [6,2,8]
filter not  [False,True,False]  ~>*  [False,False]

Ejemplo de evaluación

La función filter se puede, igual que la función map, representar por el túnel. Sin embargo, funciona de otra manera.

El modelo de tren	Haskell
Tenemos una función estaLleno que comprueba si el coche en el que está, está cargado de carbón.	Tenemos una función estaLleno que está definida de manera siguiente: estaLleno :: Bool -> Bool estaLleno True = True estaLleno False = False o en breve estaLleno :: Bool -> Bool estaLleno x = x o aún más brevemente estaLleno :: Bool -> Bool estaLleno = id
El túnel funciona de manera siguiente: Si la función estaLleno comprueba que el coche en el túnel está cargado de carbón, lo deja salir del túnel y mueve el tren. Si la función estaLleno comprueba que el coche en el túnel está vacío, lo mueve y desplaza el tren.	La función filter funciona de manera siguiente: Si toma una función p y una lista no vacía x:s, se procede de manera siguiente: Si la expresión p x se evalúa a True, el elemento x se engancha al principio de la lista final y se sigue con la evaluación de la expresión filter p s. Si la expresión p x se evalúa a False, el elemento x se tira y evalúa directamente la expresión filter p s. Si toma cualquier función y una lista vacía, se evalúa a una lista vacía.
Pongamos entonces al túnel que elige solo coches cargados, un tren de tres coches: cargado, vacío, cargado.	Apliquemos entonces la función filter a la función estaLleno y a la lista [True,False,True].
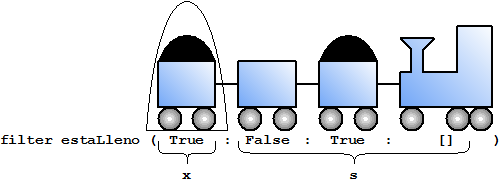
En el túnel hay un coche cargado con que queremos quedarnos también en el tren final. Entonces este coche sale del túnel y el tren se mueve.	El segundo parámetro es una lista no vacía, evaluamos según la segunda ecuación. La aplicación de la función p a x, después de la sustitución estaLleno True, se evalúa a True. Este evalúa a la parte then de la ecuación, lo que es x : filter p s. Después de la sustitución tenemos True : filter estaLleno [False,True].
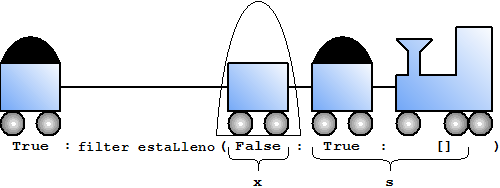
Ahora hay en el túnel un coche vacío que no queremos tener en el tren final. Entonces lo tiramos y movemos el tren.	El segundo parámetro es otra vez una lista no vacía, evaluamos según la segunda ecuación. Ya que la expresión estaLleno False se evalúa a False, la expresión if se evalúa a la parte else, es decir, a la expresión filter estaLleno [True].
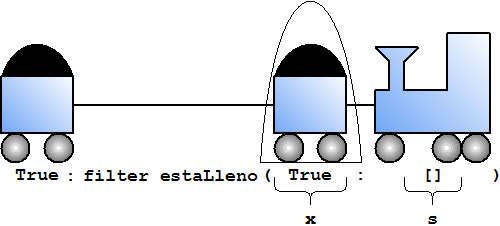
En el túnel hay un coche cargado, así que lo dejamos salir y movemos el tren.	Otra vez evaluamos según la segunda ecuación. Ahora se cumple la condición p, entonces la expresión if se evalúa a la parte then, es decir, a la expresión True : filter estaLleno [].
En el túnel está la locomotora, la dejamos pasar y ya está.	El segundo parámetro es una lista vacía, así que la evaluamos según la primera ecuación a una lista vacía.
El resultado es el tren con dos coches cargados.	El resultado es la lista de dos elementos [True,True].

Descripción

La función take x s devuelve una lista de primeros x elementos de la lista s.

Definición

Nota: Esta definición está simplificada. En realidad la función take puede tomar como el primer parámetro también un número negativo. En este caso se evalúa a una lista vacía.

take 0 _     =  []
take _ []    =  []
take n (x:s) =  x : take (n-1) s

Ejemplos

take 3 [1,2,3,4,5]       ~>*  [1,2,3]
take 4 "Hola, qué tal?"  ~>*  "Hola"
take 0 [True, True]      ~>*  []
take 5 []                ~>*  []

La expresión drop n s se evalúa a la lista s sin primeros n elementos.

Definición

drop 0 s      =  s
drop _ []     =  []
drop n (_:s)  =  drop (n-1) s

Ejemplos

drop 2 [1,2,3,4,5]    ~>*  [3,4,5]
drop 0 [1,2,3,4,5]    ~>*  [1,2,3,4,5]
drop 8 [True, False]  ~>*  []

La función repeat x crea una lista infinita de x.

[x,x,x,x,x,x,x, ... ]

Definición

repeat   ::  a -> [a]
repeat x  =  x : repeat x

Ejemplos

repeat 1              ~>*  [1,1,1,1,1, ... ]
repeat 'c'            ~>*  "ccccccccc ... "
repeat [True, False]  ~>*  [[True, False],[True, False], ... ]

Nota

Si dejamos Hugs evaluar por ejemplo la expresión repeat 1, Hugs va a imprimir indefinidamente la lista de unos hasta que lo interrumpimos pulsando Ctrl+C.

replicate n x crea una lista de n elementos de x.

Definición

replicate     ::  Int -> a -> [a]
replicate n x  =  take n (repeat x)

Ejemplos

replicate 4  1          ~>*  [1,1,1,1]
replicate 3  "Haskell"  ~>*  ["Haskell","Haskell","Haskell"]
replicate 10 'c'        ~>*  "cccccccccc"