Haskell Hero

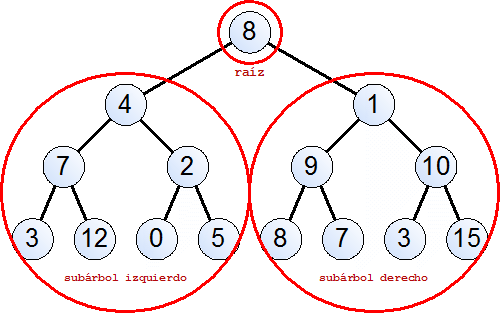Un árbol binario

Un árbol binario es una estructura de datos. Puede estar vacío o no vacío. Un árbol no vacío consta de

• un raíz y un valor en el raíz
• un subárbol izquierdo
• un subárbol derecho

En Haskell definimos árboles de manera siguiente:

data BinTree a  =  Empty  |  Node a (BinTree a) (BinTree a)

Node a (BinTree a) (BinTree a)

Ejemplos de árboles binarios de tipo BinTree Int

Ejemplo

Definid la función size :: BinTree a -> Int de tal manera que la expresión size tree se evalúe al número de nodos del árbol tree.

¿Cómo empezar? La mayoría de las funciones aplicadas a árboles binarios se define de manera siguiente:

• Si el árbol está vacío, evalúate a un valor concreto.
• Si el árbol no está vacío, aplica la función de manera recursiva al subárbol izquierdo y al subárbol derecho. El resuldado consta de estos resultados y del valor del raíz. Evalúa este resultado.

Podemos entonces escribir la definición:

size              ::  BinTree a  ->  Int
size Empty         =
size (Node x l r)  =

¿Cuántos nodos hay en un árbol vacío? Exactamente cero. Podemos entonces completar la primera ecuación.

size Empty  =  0

¿Cuántos nodos hay en un árbol no vacío? Esta pregunta no es tan fácil contestar. Miremos de que disponemos. Tenemos el valor del raíz, el subárbol izquierdo y el subárbol derecho. Nada más.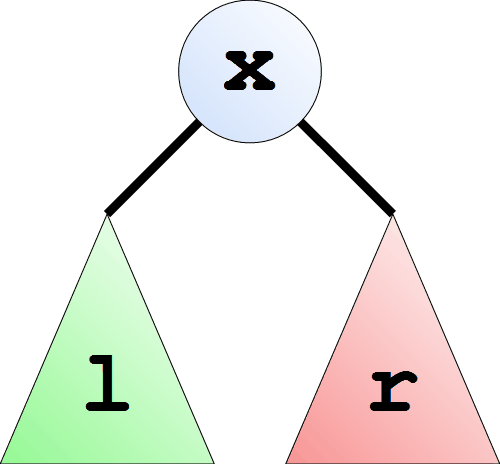

¿Cuántos nodos hay en tal árbol? Exactamente tantos cuantos están en el raíz, en el subárbol izquierdo y en el derecho en total. Entonces vamos a contar los nodos en el subárbol izquierdo de manera recursiva, lo mismo con el subárbol derecho y después añadimos uno por el raíz. Y de esta manera lo también vamos a escribir.

size (Node x l r)  =  size l  +  size r  +  1

size              ::  BinTree a  ->  Int
size Empty         =  0
size (Node _ l r)  =  size l  +  size r  +  1

La evaluación modelo

Vamos a mostrar ahora como se cuentan nodos en un árbol de tres nodos.

size (Node 5                  -- x
        (Node 2 Empty Empty)  -- l
        (Node 4 Empty Empty)  -- r
      )

~>  size (Node 2 Empty Empty) + size (Node 4 Empty Empty) +  1

~>  size Empty + size Empty + 1 + size (Node 4 Empty Empty) +  1

~>       0     + size Empty + 1 + size (Node 4 Empty Empty) +  1

~>       0     +      0     + 1 + size (Node 4 Empty Empty) +  1

~>  0 + 0 + 1 + size Empty + size Empty + 1 +  1

~>  0 + 0 + 1 +      0     + size Empty + 1 +  1

~>  0 + 0 + 1 +      0     +      0     + 1 +  1

~>* 3

Además de árboles binarios podemos también definir árboles n-arios. Difieren de árboles binarios en el hecho de que todos los nodos pueden tener un cualquier número de hijos/descendientes. Por ejemplo la estructura de directorios típica está en forma de un árbol n-ario.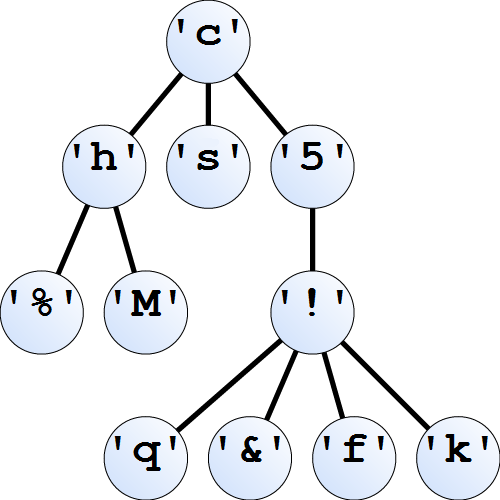

Un ejemplo de un árbol n-ario de tipo NTree Char

En Haskell definimos árboles n-arios de manera siguiente:

data NTree a  =  Nnode a [ NTree a ]

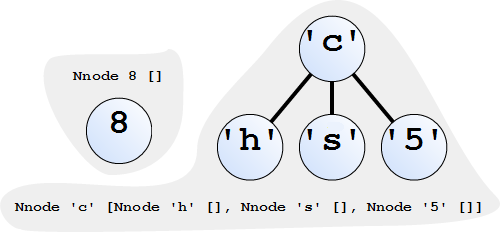Ejemplos de árboles n-arios

Fijémonos en el hecho que el árbol vacío no está definido. Si estara definido, la notación de árboles sería ambiguo. Por ejemplo un árbol de un nodo se podría definir de manera siguiente:

data NTree a  =  Empty  |  Nnode a [ NTree a ]

Nnode 3 []
Nnode 3 [Empty]
Nnode 3 [Empty, Empty]
Nnode 3 [Empty, Empty, Empty]
Nnode 3 [Empty, Empty, Empty, Empty]
...

Ejemplo

Definid la función treeSum :: NTree Integer -> Integer que suma todos valores de todos nodos en un árbol n-ario.

Mirando la estructura de un árbol n-ario podemos proceder de manera siguiente:

• sumamos de manera recursiva todos valores en todos subárboles
• sumamos todos valores contados
• sumamos el valor del raíz al resultado

Para la suma recursiva de todos árboles en la lista de subárboles utilizamos la función map, para la suma de estos valores luego utilizamos la función sum. Al fin solo sumamos el valor del raíz.

treeSum             ::  NTree Integer -> Integer
treeSum (Nnode x s)  =  sum (map treeSum s)  +  x

La evaluación modelo

treeSum (Nnode 5 [
             Nnode 4 [],
             Nnode 6 [],
             Nnode 8 []
         ])

~>   sum (map treeSum [ Nnode 4 [], Nnode 6 [], Nnode 8 [] ]) + 5

~>*  sum              [      4    ,      6    ,      8     ]  + 5

~>*                             18                            + 5

~>   23