 Haskell Hero
Haskell Hero
Haskell Hero es un manual interactivo del lenguaje Haskell para principiantes.
|
|
Tipos III¿Por qué clases de tipos?
Ya sabemos de las lecciones anteriores sobre tipos que un tipo es una caja de valores relacionados. Por ejemplo
¿Qué es el tipo de la función
¿Cómo hacer entonces la declaración de tipo de Cajas de cajas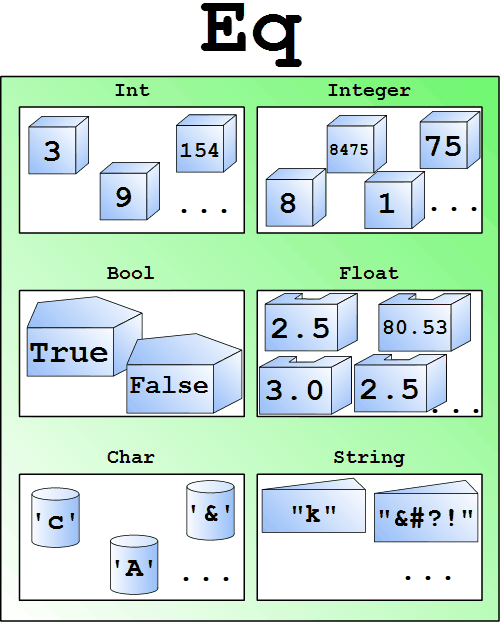 La representación de la clase de tipo Eq
Esta es la caja (==) :: Eq a => a -> a -> Bool Es decir, la función (==) puede tomar dos parámetros de cualquier tipo que está en la clase de tipos Eq.
¿Qué es el tipo de la función 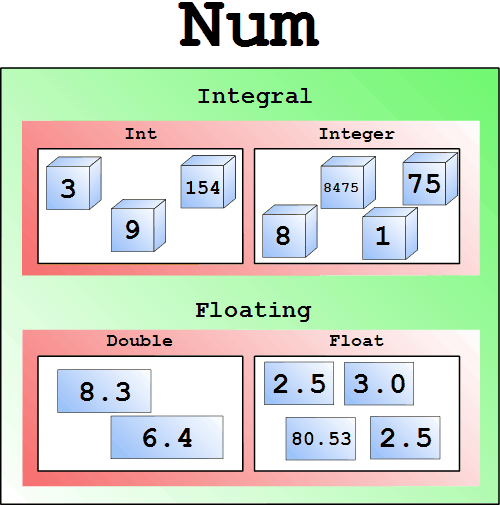 La representación de la clase de tipo Num
El tipo de la función (+) :: Num a => a -> a -> a La clase Num contiene entre otras cosas también subclases Integral, lo que son todos números enteros, y Floating, lo que son todos números decimales. Para nosotros es suficiente conocer la caja Num.
Nos queda mencionar la caja
Operadores (<) :: Ord a => a -> a -> Bool Insertamos cajas en cajas
Ahora ya sabemos que hay funciones que toman como parámetro "cualquier cosa que se puede comparar por igualdad". Por ejemplo la función
zipWith (==) :: Eq a => [a] -> [a] -> [Bool] toma dos listas de cualquier cosa comparable y devuelve una lista de valores booleanos. Nos gustaría aplicar esta función por ejemplo a dos listas de tipo [Nat], lo que son números naturales que hemos definido antes. Están definidos de manera siguiente:
data Nat = Zero | Succ Nat Nos gustaría poder evaluar esta expresión: zipWith (==) [Zero, Succ Zero] [Zero, Succ (Succ Zero)] ~>* [True, False] Sin embargo, esta evaluación no se puede realizar ya que Nat no pertenece a la clase Eq. ¿Qué va ahora? Insertamos el tipo Nat en la clase Eq. Lo hacemos definiendo la igualdad de dos valores de tipo Nat.
¿Cuándo son iguales dos valores de tipo
Lo vamos a definir de esta manera. Primero hay que mencionar que hacemos. Insertamos el tipo instance Eq Nat Completamos la definición de igualdad de dos valores de tipo Nat según la descripción mencionada arriba.
instance Eq Nat
where Zero == Zero = True
Succ x == Succ y = x == y
_ == _ = False
En la ecuación Succ x == Succ y = x == y en la parte derecha la misma función se llama por medio de == de manera recursiva ya que x y y son también de tipo Nat, es decir, pueden solo estar en forma Zero o Succ x.
Y ya está. Ahora podemos usar valores de tipo
Si el tipo está en la clase de tipo
|